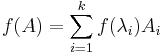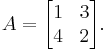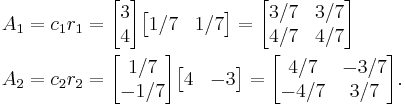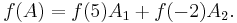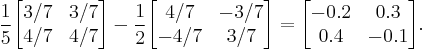Sylvester's formula

In matrix theory, Sylvester's formula or Sylvester's matrix theorem (named after J. J. Sylvester) expresses an analytic function f(A) of a matrix A in terms of the eigenvalues and eigenvectors of A.^[1]^[2] It states that

$f(A) = \sum_{i=1}^k f(\lambda_i) A_i$

where the λ_i are the eigenvalues of A, and the matrices A_i are the corresponding Frobenius covariants of A.

Sylvester's formula is only valid for diagonalizable matrices; an extension due to Buchheim covers the general case.

Conditions

Sylvester's formula applies for any diagonalizable matrix A with k distinct eigenvalues, λ₁, …, λ_k, and any function f defined on some subset of the complex numbers such that f(A) is well defined. The last condition means that every eigenvalue λ_i is in the domain of f, and that every eigenvalue λ_i with multiplicity m_i > 1 is in the interior of the domain, with f being (m_i − 1) times differentiable at λ_i.^[1]^:Def.6.4.

Example

Consider the two-by-two matrix:

$A = \begin{bmatrix} 1 & 3 \\ 4 & 2 \end{bmatrix}.$

This matrix has two eigenvalues, 5 and −2. Its Frobenius covariants are

$\begin{align} A_1 &= c_1 r_1 = \begin{bmatrix} 3 \\ 4 \end{bmatrix} \begin{bmatrix} 1/7 & 1/7 \end{bmatrix} = \begin{bmatrix} 3/7 & 3/7 \\ 4/7 & 4/7 \end{bmatrix} \\ A_2 &= c_2 r_2 = \begin{bmatrix} 1/7 \\ -1/7 \end{bmatrix} \begin{bmatrix} 4 & -3 \end{bmatrix} = \begin{bmatrix} 4/7 & -3/7 \\ -4/7 & 3/7 \end{bmatrix}. \end{align}$

Sylvester's formula then states that

$f(A) = f(5) A_1 %2B f(-2) A_2. \,$

For instance, if f is defined by f(x) = x⁻¹, then Sylvester's formula computes the matrix inverse f(A) = A⁻¹ as

$\frac{1}{5} \begin{bmatrix} 3/7 & 3/7 \\ 4/7 & 4/7 \end{bmatrix} - \frac{1}{2} \begin{bmatrix} 4/7 & -3/7 \\ -4/7 & 3/7 \end{bmatrix} = \begin{bmatrix} -0.2 & 0.3 \\ 0.4 & -0.1 \end{bmatrix}.$

References

^ ^a ^b Roger A. Horn and Charles R. Johnson (1991), Topics in Matrix Analysis. Cambridge University Press, ISBN 9780521467131
^ Jon F. Claerbout (1976), Sylvester's matrix theorem, a section of Fundamentals of Geophysical Data Processing. Online version at sepwww.stanford.edu, accessed on 2010-03-14.